| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Flutter
- 42경산
- Regression
- map
- RNN
- 피플
- AI
- 지정헌혈
- 유데미
- 앱개발
- filtering
- 자연어처리
- Computer Vision
- 선형대수학
- mnist
- 파이썬
- 모델
- 코딩애플
- 크롤링
- 42서울
- 플러터
- 선형회귀
- 데이터분석
- CV
- 크롤러
- 인공지능
- 머신러닝
- 딥러닝
- 회귀
- pytorch
- Today
- Total
David의 개발 이야기!
[선형대수학] 1.5 Solution Sets of Linear Systems 선형계의 해의 집합 본문
제차 선형계(homogeneous system)
자명해(trivial solution)
비자명해(nontrivial solution)
비제차 선형계(nonhomogeneous system)
특수해(particular solution), 제차해(homogeneous solution)
제차 방정식과 비제차 방정식의 관계
에 대해서 알아보자
1. 제차 선형계 - Homogeneous Linear Systems
Ax=0 인 행렬 방정식(matrix equation)을 제차 선형계(Homogeneous linear system)라고 한다.
제차 선형계의 특징
(1) 항상 최소 하나의 자명해(trival solution)을 갖고 있다.
자명해(trival solution)은 x=0을 의미한다.
(2) 비자명해(nontrivial solution)를 갖는 조건
방정식이 1개 이상의 자유 변수(free variable)를 갖고 있으면 비자명해(nontrivial solution)을 갖게 된다.
nontrivail solution은 x=0이 아닌 것을 의미한다.
이는 이론2에서 free variable이 없으면 unique solution을 갖고, free variable이 있으면 infinitely many solutions를 갖는 것과 비슷하다.
2. 비자명해(nontrivial solution)이 있는지 확인하기
Ax=0을 augmented matrix로 표현하고 row reduction을 통해 reduced echelon matrix를 만들어서 free variable를 갖고 있는지 확인해 보면 된다.
linear system
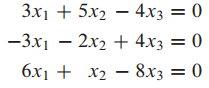
augmented matrix , row reduction, ehelon form

reduced echelon form

는 basic solution, 는 trival solution, 은 free variable인 것을 도출했다.

이는 x1,x2,x3을 x3하나로 표현할 수 있기 때문에 하나의 벡터의 선형 결합으로 표현할 수 있다.
Span{v}를 의미하며 직선으로 표현된다.
Span{v}로 표시할수 있다는 의미는 nontrival solution가 존재한다는 것을 의미한다.
trivial solution은 x=0을 의미하므로 x에 해당하는 v가 사라지기 때문이다.
3. 선형 방정식이 하나 일때 비자명해(nontrivial solution) 확인하기
선형 방정식이 하나인 경우를 확인해보자.
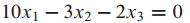
식이 하나여도 linear system이라고 부를 수 있다.
을 pivot position으로 설정하고 풀면 된다.
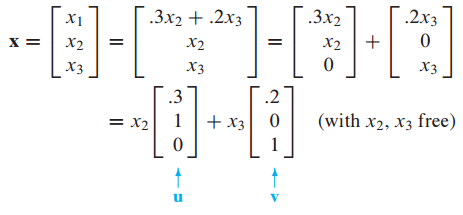
x1은 basic solution, x2,x3은 free variables 이다.
따라서 nontrivial이 존재하며 두 개의 벡터의 선형 결합으로 표현할 수 있으므로 Span{u,v}가 된다.
이는 평면으로 표현할 수 있다.
4. 제차 선형계 정리 - Homogeneous linear system
Ax=0 제차 선형계에서 해의 집합은 Span{v1,...,vp}로 표현할 수 있다.
만약 trivial solution이 존재하면 Span{0}으로 표현한다. (n공간에서 하나의 점 이므로)
따라서 nontrivial solution이 없다면 Span{v1,...,vp}로 표현할 수 없다.
+ Parametric Vector Form

5. 비제차 선형계 - Nonhomogeneous Linear Systems
비제차 선형계(Nonhomogeneous linear system)은 Ax=b를 의미한다.
b는 nonzero vertor을 의미하며 이는 b의 entry 중 적어도 하나 이상의 entry가 nonzero를 의미한다
비제차 선형계 문제를 한번 풀어보면,
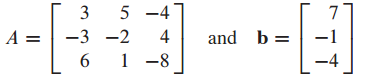
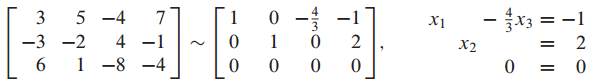
여기서 은 basic variables, 는 nontrvial solution, 은 free variable입니다.
x를 vector로 표시하면 다음과 같습니다.
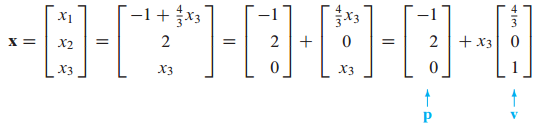
p를 특수 해(particular solution), v를 제차 해(homogeneous solution)라고 한다.
비제차 선형계의 해는 p(특수해)와 v(제차해)의 합으로 표현된다.
이처럼 제차 선형계와 비제차 선형계는 밀접한 관계를 갖고 있다.
6. Theorm 6. 비제차 방정식의 해의 집합
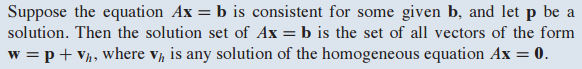
비제차 방정식의 해의 집합은 w=p+로 표현된다.
여기서 는 제차 방정식의 해다.
7. 제차 해와 비제차 해의 관계 (Parallel)
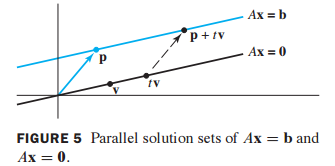
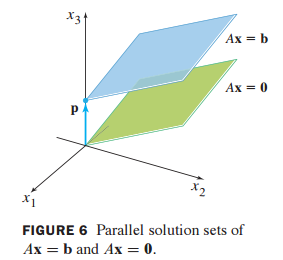
이 의미는 제차 해와 비제차 해는 평행 관계를 의미한다.
Ax=b, Ax=0의 해는 p(particular solution)에 의해 평행 관계를 이루게 된다.
그리고 v(homogeneous solution)은 평면 공간을 의미한다.




