| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Flutter
- 자연어처리
- Computer Vision
- Regression
- mnist
- 모델
- RNN
- map
- 지정헌혈
- 선형대수학
- 앱개발
- 파이썬
- 데이터분석
- pytorch
- 유데미
- 42서울
- 42경산
- 크롤링
- 선형회귀
- 플러터
- 코딩애플
- 피플
- AI
- filtering
- 인공지능
- CV
- 딥러닝
- 크롤러
- 머신러닝
- 회귀
- Today
- Total
David의 개발 이야기!
[선형대수학] 1.4 행렬방정식 Ax=b, Matrix of Equation 본문
오늘 정리할 것은 다음과 같다
행렬방정식(matrix equation)
Ax = b
Theorm 3 선형시스템을 나타낼수 있는 3가지 방법
Theorm 4
행렬방정식을 빠르게 계산하는 내적
1. Ax 의 의미 : product of A and X

이것은 x를 weights로 사용한 A의 columns의 linear combination 임.
즉, x는 scalar의 vector 이다.
(1) 벡터방정식을 행렬방정식으로 표현하는 방법 : Vector equation to matrix equation

(2) 행렬방정식 푸는 방법!!!! 꼭 숙지하기!!

(3). 선형 시스템을 행렬 방정식으로 표현
- system of linear equations to matrix equation
linear system
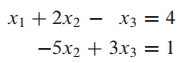
vector equation
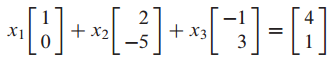
matrix equation
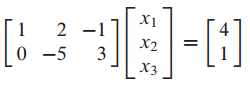
(4) 행렬 방정식을 계산하는 효과적인 방법 - more efficient way to compute matrix equation
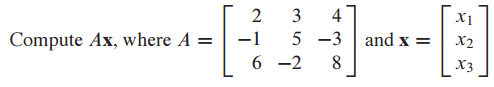
기존 방법은 행렬 방정식을 벡터 방정식으로 변환해서 푸는 것임.
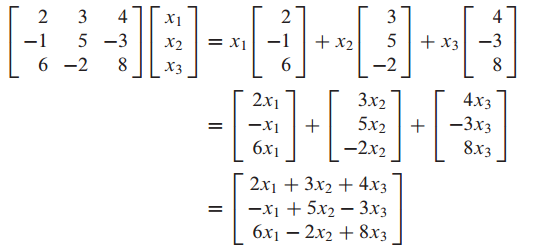
내적을 이용하면 빠르게 풀 수 있다.
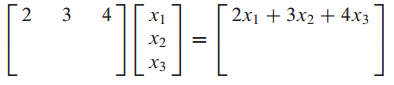
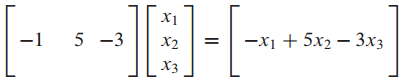
Theorm 3
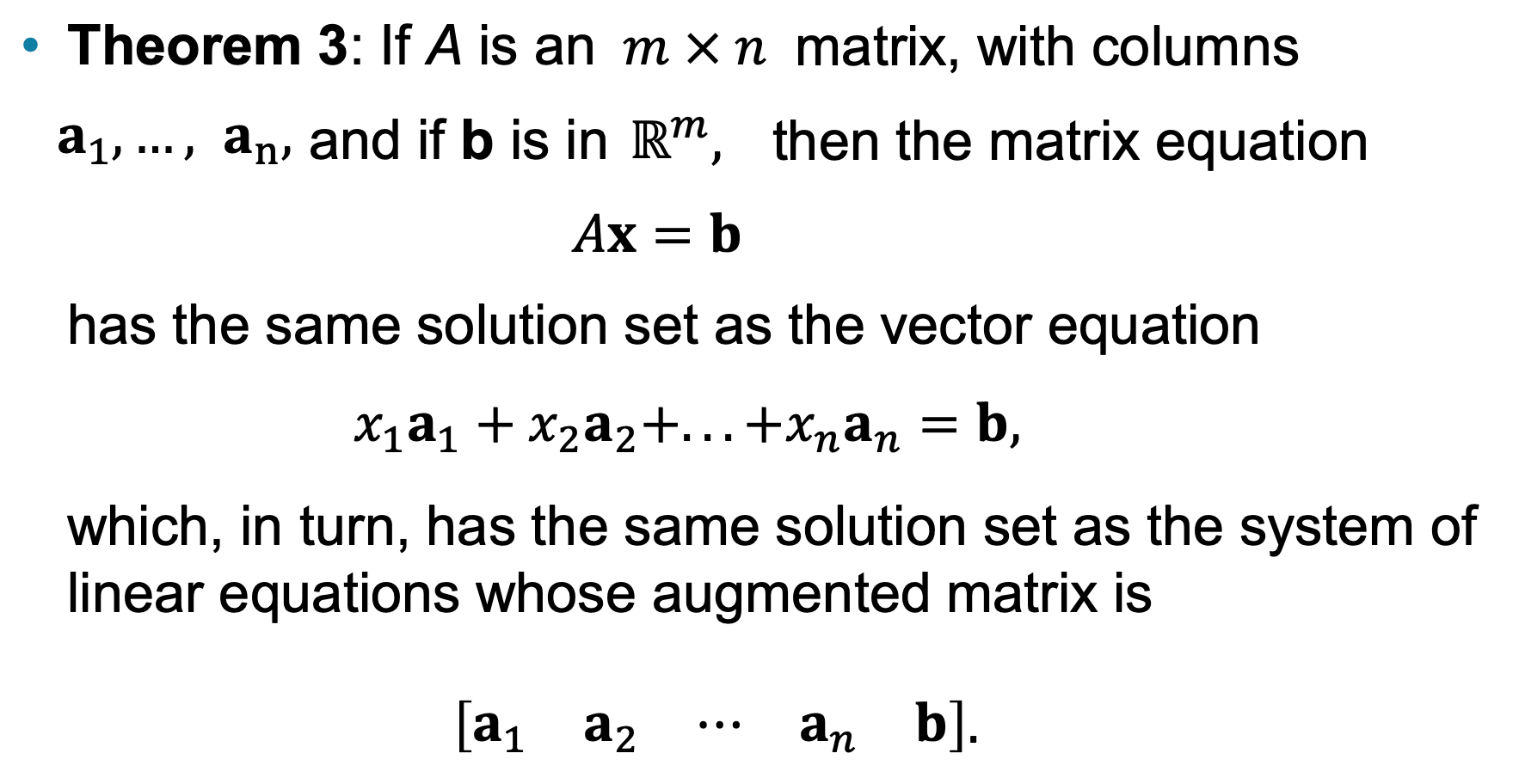
linear system을 3가지로 표현할 수 있으며 이 3가지는 모두 동일한 해를 갖는다.
(1) 행렬 방정식(matrix equation)
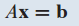
(2) 벡터 방정식(vector equation), 선형 결합(linear combination)

(3) 첨가 행렬(augmented matrix)

Theorm 4

a. For each b in , the equation Ax=b has a solution
Rm 공간에 있는 임의의 b에 대해서 Ax=b(matrix equation)은 solution을 갖고 있다.
b. Each b in is a linear combination of the columns of A
공간에서 b는 A의 columns의 선형 결합이다.
c. The columns of A span
A의 열들은 공간에서 span 이다. -> linear combination을 의미
d. A has a pivot position in every row
A는 모든 행에 pivot position을 갖고 있다.
A는 coefficient matrix를 의미한다.
A의 행에 pivot position이 없다면 b가 pivot position이 된다.
이는 no solution을 의미한다.
8. Theorm 5

A는 계수 행렬(coefficient matrix)
u, v는 벡터
c는 스칼라 .




